液体のエントロピーの第一原理計算に成功

• 液体のエントロピー^※1を、原子種の指定のみで計算する方法を開発
• これまでは、液体のエントロピーには標準理論がなく、どう計算するかは手探りの状態であった
• 液体を利用した物質合成プロセスにおける化学反応は経験的にしか分からなかったが、本研究成果はそれらの理論予測を可能にするものであり、広く工業社会へのインパクトが期待される

　大阪大学産業科学研究所 白井光雲招へい教授の研究グループは、液体のエントロピーについて、経験的パラメータを用いることなく計算する方法を開発しました。

　これまで、液体のエントロピーの計算には標準理論というものがなく、どう計算するかはほとんど手探りの状態でした。そのため、液体を含む化学反応は精度の高い予測ができていませんでした。

　今回の研究成果により、液体に対してあらゆる種類の実験データを参照することなく、原子種の指定のみという理論の枠内でエントロピーが計算できるようになりました。これにより、液体を利用した物質合成プロセスは理論予測が可能なものとなり、結晶成長、精練、触媒処理ほか、液体を使うあらゆる分野において新しい合成方法などが提案・発見されるものと期待されます。

　本研究成果は、IOP Publishing社の科学誌 『Journal of Physics: Condensed Matter』 (オンライン)に、7月15日（火）（現地時間）に公開されました。

　エントロピーは、エネルギーとともに、物質の性質の中で最も重要なパラメータです。しかしエネルギーとは違い、エントロピーは抽象的な概念で、教科書、解説書で何度となく説明されるものの、なかなか分かった気がしない、物理の中で最も分かりにくい量です。大抵は「無秩序の程度を表す」という解釈で一応の納得をします。しかし多様な物質の中で、無秩序とは何かということになると、専門家でもよく分からなくなります。DNAの核酸配列の意味を知らなければ、それは単なる乱雑な配置に過ぎず、エントロピーは大きいということになってしまいますが、生命体の設計図が乱数表であるはずはありません。

　解釈はともかく、物質のエントロピーはきちんと測定され、その値はハンドブックにリストアップされております。したがって、理論家に問われているのは、それら実験値をきちんと再現することです。エントロピー（S）は、従来、統計力学において、分配関数という量を計算することで得ております。気体に対してはその計算は簡単です。また、固体の場合は、フォノン^※2というものに対して分配関数を計算することでエントロピーが計算できます。しかし、液体は気体と固体の中間の相で、どちらの計算も使えず、信頼に足る方法がありませんでした。気体状態から出発し摂動理論を適用することが行われておりましたが、収束するのかどうかは不明です。フォノンから出発する方法もありますが、いろいろ難点を抱えております。合金溶液のエントロピーを予測することは現在不可能です。

　以上の難題を抱えている液体のエントロピー計算を、本研究ではエントロピーの熱力学的定義を用いることで一気に解決しました。熱力学ではSは比熱^※3（C）を温度（T）で積分することで求められます。正確にはS=∫(C/T)dTです。世紀の難問がこのように誰でも知っている式で解決することに拍子抜けしますが、本当に困難な点は、液体に対する比熱の計算方法です。

　比熱は、エントロピーと同様、液体の場合は標準理論というものがありません。液体の性質の何を計算したら比熱の計算になるのか、雲を掴むような難しさがあります。固体の場合は、結晶構造という構造があり、それを知ればその固体の性質が分かります。しかし液体には構成する原子種以外にはっきりとした構造というものがなく、何がその比熱を決めるのかよく分からないのです。固体との類推で、液体でもフォノンがあるとして強引に計算する方法もありますが、根本的な困難さがあります。それはCの温度依存性です。フォノンのモデルでは、CはTとともに増加し、ある温度以上では飽和し一定になります。減少することはありません。しかし液体の比熱では、CはTとともに減少するのです。そこでフォノンのモデルでは、人為的なパラメータを導入し実験と合わせるのですが、物理的根拠は薄弱です。
この問題に対し、本研究では、液体の比熱をフォノンモデルによらず、液体の全エネルギーから近似なしに厳密に計算できることを示しました。全エネルギーの計算自体は、現在、第一原理計算という理論枠が広く知られ、それにより精度の高い計算が可能となっております。熱力学的内部エネルギー（U）は、分子動力学（MD）シミュレーション^※4によってTの関数として求められます。比熱はUをTで微分することで求められます。重要なことは、MDシミュレーションでよく用いられる熱浴というものを入れず断熱シミュレーションにすることです。これにより原子のエネルギー緩和過程が正確なものになります。

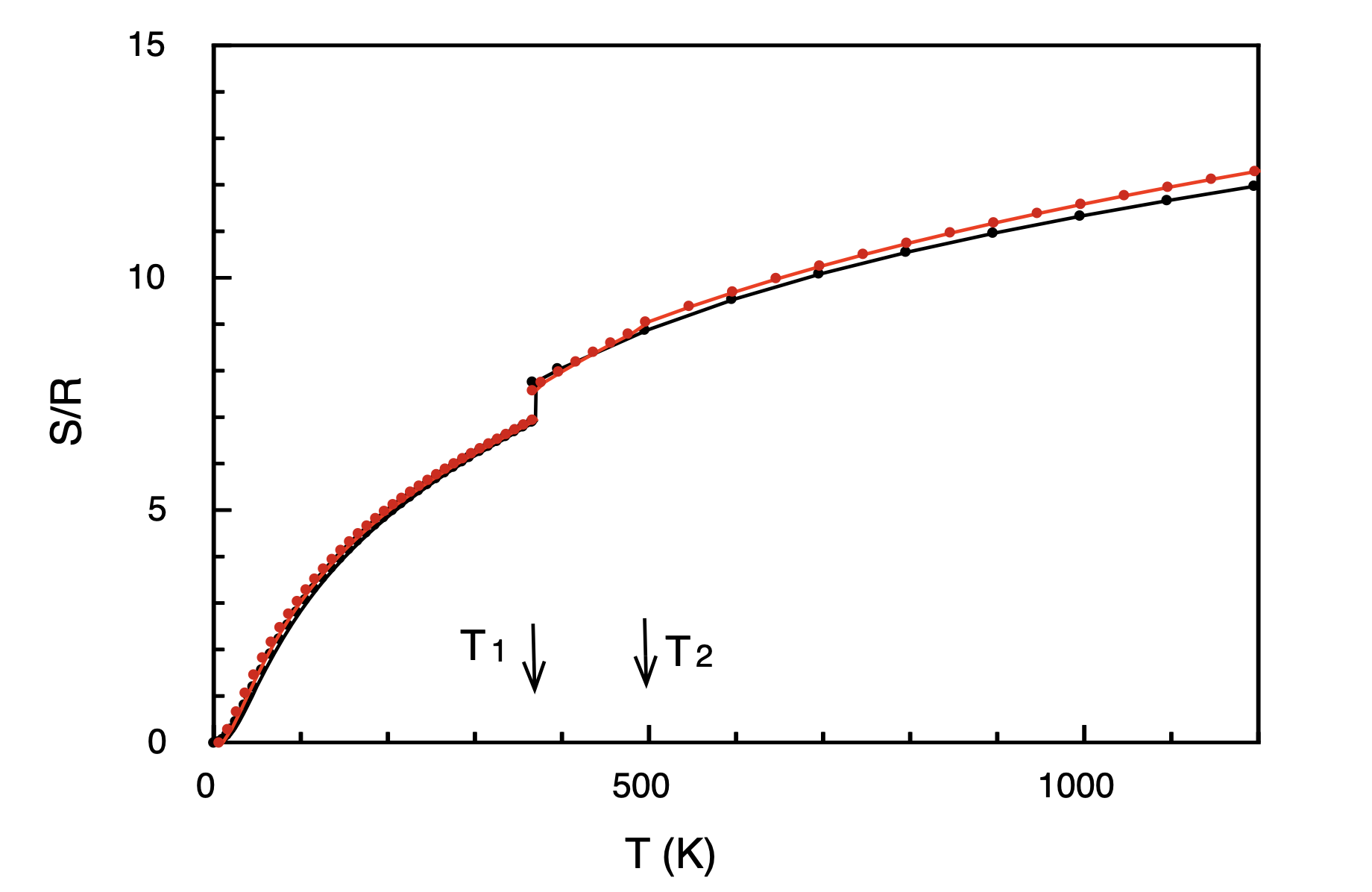
　この方法により、液体の比熱の負の温度依存性が経験的パラメータを導入することなしに、初めて再現されました。比熱の負の温度依存性は原子のエネルギー緩和に起因することが分かりました。液体の比熱が正確に再現できれば、それを積分したエントロピーも実験をよく再現します（図）。

　本方法は第一原理計算とMDシミュレーションを組み合わせたもので、方法論的には誰にでも使えて、物質によらず汎用性のあるものです。今日、物質科学の分野で、温度・圧力の広い範囲にわたり液体の自由エネルギーの値が求められております。高融点固体を低温度で作成する場合にどの温度まで下げられるかは、経験的にしか分かっておりません。液体を利用した化学反応が起きるかどうかは自由エネルギーの変化によって決まりますが、そのデータが不足しているため理論予測ができないのです。液体の自由エネルギーの計算で一番の障害となっているのは、エントロピーの計算です。したがって液体のエントロピーの計算が可能となれば、その自由エネルギーも予測可能となり、液体を利用する化学反応の理論予測が可能となります。液体を利用したプロセスは工業社会の至る所で行われているので、その応用はとてつもなく広がっています。まだMDシミュレーションは手軽にすぐ計算できるものではありませんが、原理的に可能になったということは、この分野でのブレークスルーになると考えられます。

　本研究成果は、2025年7月15日（火）（現地時間）にIOP Publishingが発行する科学誌 『Journal of Physics: Condensed Matter』 に掲載されました。
タイトル：“First-principles calculation of the entropy of liquids with a case study on sodium”
著者名：Koun Shirai, Hiroyoshi Momida, Kazunori Sato and Sangil Hyun
DOI：https://doi.org/10.1088/1361-648X/ade83e

※1　エントロピー
物質のエネルギーは、それがいくら大きくとも利用できなければエネルギー資源としての価値はない。その価値を決めるものがエントロピー（S）。あらゆる種類のエネルギー資源は、使えば必ず価値が下がる。Sは劣化の程度を示す。微視的には無秩序の程度を表すと解釈される。物質は、放っておけば必ず無秩序さを増す。それを言い表したものが熱力学の第二法則である。

※2　フォノン
結晶を構成する原子は規則的に配置されている。その原子位置は固定されている（平衡位置と呼ばれる）が、微視的に見るとその平衡位置の周りに常に揺らいでいる。その揺らぎ量を表すものがフォノン。揺らぎ幅は温度（T）で決まり、それが比熱を決める。

※3　比熱
物質の加熱・冷却のしにくさを表す物理量。物質の単位量あたり、温度を1度上げるのに要する熱量で定義される。

※4　分子動力学（MD）シミュレーション 
固体や液体は多数個の原子が集まったものである。その集団が有限温度でどのような振る舞いをするかをn個の構成原子を使ってシミュレーションするものである。原子の運動は、ニュートンの運動方程式から、直接時間の関数として得られる。原子に働く力は、第一原理分子動力学法では量子力学から求めるので経験的なパラメータは入らない。