研究成果のポイント
概要
大阪大学産業科学研究所の下出敦夫准教授、南谷英美教授の研究グループは、スピントロニクスの分野で次世代不揮発性メモリへの応用が期待される「スピンホール効果」に関し、その新たな性能指標を実材料に対して高精度に計算するためのプログラムを開発しました。
スピンホール効果は、スピン軌道相互作用※4の大きい物質(貴金属や半導体)に電場をかけたとき、電場と垂直方向にスピンの流れが生じる現象として理解されています。これまでスピンホール効果は、電場とスピン流の比であるスピンホール伝導度とよばれる指標を用いてその性能が評価されてきました。これは、電気的にスピン流を取り出す効率を示す指標であり、その指標が大きい物質ほど、省エネ・高速化を目指す上で、よりスピントロニクスデバイスに適した材料と判断することができます。
ところが、スピン軌道相互作用がある場合、スピンは物質の中で回転したり、消えたり、湧き出したりするため、スピン流を一意に定義することができません。デバイスへの応用を目指すうえで「巨大な」スピンホール効果を示す物質を探索したいところですが、巨大かどうかを測るスピンホール伝導度はスピン流の定義のしかたによって変わってしまうのです。
今回、研究グループは、スピンホール効果の新たな性能指標であるスピン蓄積係数の第一原理計算を行うためのプログラム『postw90-spin』を開発しました。これはスピンホール効果によってスピンが蓄積する現象(図)を特徴づける性能指標で、スピン流を用いていないため定義の不定性がありません。これにより、スピンホール効果に対しあいまいさのない性能評価が可能になり、高速・低消費電力・高耐久性を備えた次世代不揮発性メモリの実現に適した物質探索が一層進むことが期待されます。
本研究成果は、英国科学誌『npj Spintronics』(オンライン)に、7月10日(木)に公開されました。
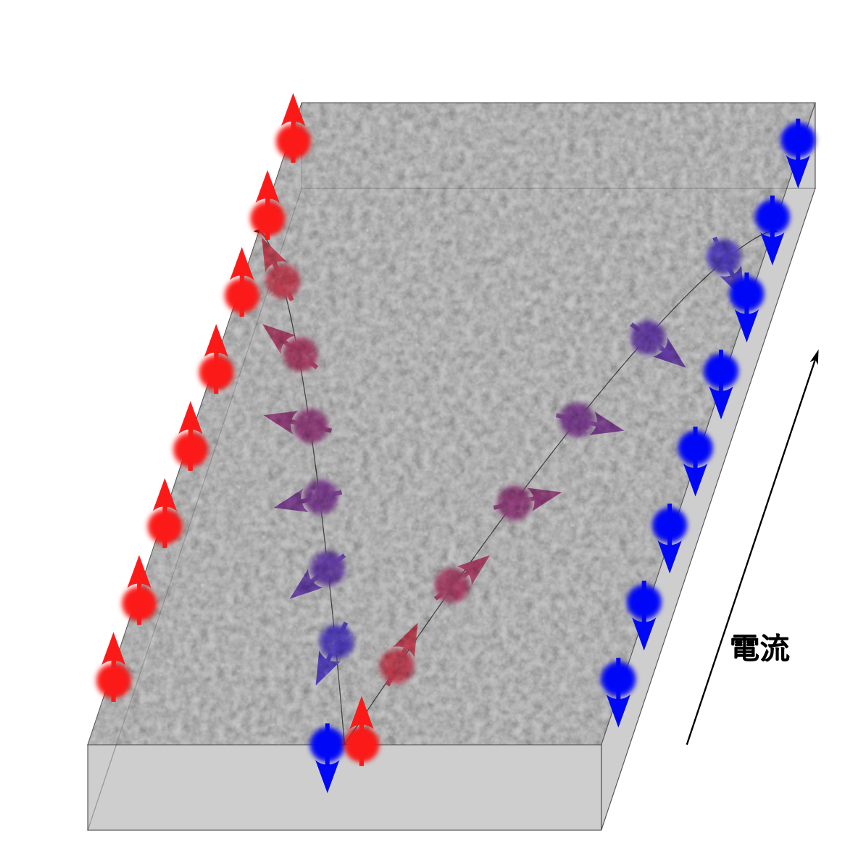
スピン流の定義の不定性は、スピンホール効果の研究者のおそらく誰もが認識しながら、それ以外の方法が困難であるという理由から目を背けてきた問題であると考えています。この問題に対して一定の解答を与え、さらに実材料に対して予測する方法を確立できたことは、スピンホール効果の微視的理解を大きく進め、スピントロニクスの実験と理論をつなぐ架け橋になると期待しています。
研究の背景
スピンは磁石の起源で、S極からN極への向きをもっています。スピン軌道相互作用によって、スピンは物質の中で回転したり、消えたり、湧き出したりしており、スピンの流れ、すなわちスピン流は保存しないといわれています。例えば、水道管を流れてくる途中で水が消えてしまうとしたら、水道の使用量を正しく測ることができないように、保存しないスピン流を一意に定義することはできないのです。スピン流の定義のしかたによって値が変わるスピンホール伝導度は、性能指標としては不完全といえます。
この問題に対し、研究グループでは以前から、スピンホール効果によって試料の両端に蓄積するスピンに着目していました。スピン蓄積とよばれるこの現象は、スピン流が試料の端に流れ込んでスピンへと緩和することで起こると解釈されていますが、実験ではその過程はいまだ観測されておらず、端に蓄積したスピンが観測されているのみです(図)。本研究の前段階として、電場勾配と蓄積するスピンの比であるスピン蓄積係数をスピンホール効果の新たな性能指標として提案し、半導体を記述する簡単なモデルに対して計算を行いました。試料の端には電場勾配が存在しますが、スピン蓄積係数そのものは端のない境界条件で評価できるということがポイントです。次のステップとして、実材料に対して計算を行う方法の確立とプログラムの開発を目指しました。
研究の内容
研究グループでは、密度汎関数理論※5と最局在ワニエ関数法※6を組み合わせ、実材料に対してスピン蓄積係数の第一原理計算を行う方法を確立しました。密度汎関数理論は物質の電子状態を高精度に計算するための枠組みですが、計算コスト(時間やメモリ使用量)が高いという欠点があります。そのため、スピンホール伝導度やスピン蓄積係数といった物理量を計算することは非常に困難です。最局在ワニエ関数法を経由することで、密度汎関数理論によって得られた電子状態を内挿することが可能になり、計算コストを大きく削減することができます。開発したプログラムを用いて、単層二硫化モリブデン(MoS2)とテルル(Te)に対して計算を行いました。
通常、第一原理計算では、端のない境界条件を課すことで計算コストを削減しています。スピン蓄積は電場をかけた状態で試料の端で起こる現象なので、このような端のない境界条件のもとで計算することは不可能です。また、端のある境界条件では膨大な計算コストを要します。スピン蓄積係数という、端のない境界条件で評価可能な性能指標を定義したことで、はじめて実材料に対する計算が可能になりました。このプログラム『postw90-spin』は世界的に利用されている最局在ワニエ関数法のパッケージ 『Wannier90』 をもとに実装しており、Github上で公開しています。
本研究成果が社会に与える影響(本研究成果の意義)
スピンホール効果は、次世代磁気メモリとして注目される、スピン軌道トルク型磁気抵抗ランダムアクセスメモリ(SOT-MRAM)の基礎となる現象です。本研究成果により、スピン流の定義の不定性を回避したスピンホール効果の性能予測が可能になりました。今後、さまざまな実材料に対して計算を行うことにより、高速に動作するSOT-MRAMのための物質探索が進むことが期待されます。
特記事項
本研究成果は、2025年7月10日(木)に英国科学誌 『npj Spintronics』 (オンライン)に掲載されました。
タイトル:“Wannier interpolation of spin accumulation coefficient”
著者名:Atsuo Shitade and Emi Minamitani
DOI:https://doi.org/10.1038/s44306-025-00096-x
用語説明
※1 スピントロニクス
スピンとエレクトロニクスを組み合わせた造語。電子がもつ電荷の自由度だけでなく、電子の「スピン」と呼ばれる性質も利用することで、従来のエレクトロニクスでは実現できない機能や性能を目指す研究分野。
※2 スピンホール効果
貴金属や半導体などの試料に電場をかけたとき、電場と垂直方向にスピン流が生じる現象として理解されている。実験では、試料の両端に上向きスピンと下向きスピンが生じることが観測されている。
※3 第一原理計算
実験データに頼ることなく、原子の種類と位置の情報から、物質の性質をコンピュータで計算する方法。未知の物質の性質の探索や、実験では測定のできない物理現象を調べることができる。
※4 スピン軌道相互作用
電子のスピンと軌道角運動量の間にはたらく相互作用で、一般的に重い元素で大きくなる傾向がある。これにより電子は動きながらそのスピンの向きを変化させ続けている。
※5 密度汎関数理論
電子の量子力学的な波動関数ではなく、電子密度を用いて物理量を表現する枠組み。
※6 最局在ワニエ関数法
原子に束縛された電子軌道のように、空間的に局在した波動関数を構成する方法。密度汎関数理論によって得られた波動関数の一部を精度よく再現することで、物理量の計算コストを削減することができる。

